. Untuk menyelesaikan soal-soal limit fungsi aljabar terdapat beberapa metode yang digunakan, adalah :
- Metode Subitusi
- Metode Pemfaktoran
- Metode membagi dengan pangkat tertinggi penyebut
- Metode mengalikan dengan aspek sekawan
Nah kapan kita harus menggunakan metode tersebut ?. Untuk mampu memahaminya secara lebih baik, silahkan simak pembahasan dari pola soal limit fungsi aljabar di bawah ini.
Pembahasan Soal Limit Fungsi Aljabar
Soal No.1Tentukan nilai limit fungsi aljabar di bawah ini :
Pembahasan
Soal No.2
Carilah nilai limit fungsi aljabar di bawah ini :
lim x→2
2x2 + 4 2x + 2 Pembahasan
lim x→2
2x2 + 4 2x + 2 = 2.(22) + 4 2.(2) + 2 = 12 6 = 2 Metode yang dipakai pada soal No.1 dan No.2 yaitu Metode Substitusi, dimana kita langsung memasukkan nilai peubahnya. Nah sekarang mari kita ketahui metode pemfaktoran pada soal limit fungsi aljabar di bawah ini.
Soal No.3
Hitunglah nilai limit berikut ini ?
lim x→ -1
x2 - 1 x + 1
Pembahasan
Ketika kita gunakan tata cara substitusi di peroleh :
lim x→ -1
x2 - 1 x + 1
= (-1)2 - 1 -1 + 1
= 0 0
Perhatikan kita menerima bentuk (0/0). Bentuk ini yakni bentuk terdefinisikan atau tidak tentu. Oleh alasannya adalah itu kita mesti menggunakan tata cara pemfaktoran :
lim x→ -1
x2 - 1 x + 1
= lim x→ -1
(x - 1)(x + 1) (x + 1)
⇔
lim x→ -1
(x - 1) ⇔ (-1 - 1)
⇔ -2
Soal No.4
Carilah nilai limit fungsi aljabar di bawah ini :
lim x→ 2
x2 - 4 x2 - 3x + 2
Pembahasan
Pada saat dipakai metode substitusi maka akan didapatkan :
lim x→ 2
x2 - 4 x2 - 3x + 2
= 22 - 4 22 - 3(2) + 2
= 0 0
Karena hasil yang diperoleh adalah (0/0) ialah bentuk tak tentu, maka mesti difaktorkan :
lim x→ 2
x2 - 4 x2 - 3x + 2
= lim x→ 2
(x + 2)(x - 2) (x - 2(x - 1)
⇔
lim x→ 2
(x + 2) (x - 1)
⇔
(2 + 2) (2 - 1)
⇔ 4
Pada soal No.3 dan No.4 kita menerapkan "Metode Pemfaktoran".Nah sekarang anda telah mengenail baik sistem pemfaktoran pada limit fungsi aljabar. Sehingga anda dapat mengerti perbedaan cara penerapan tata cara substitusi dengan metode pemfaktoran.
Sekarang kita lanjutkan dengan metode membagi dengan pangkat tertinggi penyebut
Sekarang kita lanjutkan dengan metode membagi dengan pangkat tertinggi penyebut
Soal No.5
Hitunglah nilai limit fungsi aljabar berikut ini
lim x→∞
4x + 1 x2 - 2 Pembahasan
lim x→∞
4x + 1 x2 - 2 Dari limit di atas :
- Derajat pangkat pembilang = 1, lihat pangkat x pada 4x
- Derajat pangkat penyebut = 3, lihat pangkat x pada x2
Cara menetukan nilai limitnya :
lim x→∞
4x + 1 x2 - 2 ⇔
lim x→∞
4x x2 + 1 x2 x2 x2 - 2 x2
⇔
lim x→∞
4 x + 1 x2 1 - 2 x2
= 4 ∞ + 1 (∞)2 1 - 2 (∞)2
= 0 + 0 1 - 0
= 0 Untuk soal no.5 kita lakukan dengan sistem metode membagi dengan pangkat tertinggi penyebut. Penyelesaian fungis aljabar dengan tata cara ini dipakai pada fungsi limit yang memiliki bentuk :
lim f(x) x→∞
Soal No.6
Carilah nilai limit fungsi aljabar berikut ini :
lim x→2
√x + 2 - √3x - 2
x - 2 Pembahasan
Dengan substitusi eksklusif :
Karena didapatkan bentuk tidak pasti dan mempunyai bentuk akar, maka sistem yang dipakai ialah perkalian akar sekawan:
(x - 2) (x - 2)(√x + 2 + √3x - 2) = -2 (√2 + 2 + √3(2) - 2) = -2 (√4 + √4) = -1 2
lim x→2
√x + 2 - √3x - 2
x - 2 = √2 + 2 - √3(2) - 2
2 - 2 = √4 - √4
0 = 0 0 Karena didapatkan bentuk tidak pasti dan mempunyai bentuk akar, maka sistem yang dipakai ialah perkalian akar sekawan:
lim x→2
√x + 2 - √3x - 2
x - 2 x √x + 2 + √3x - 2
√x + 2 + √3x - 2
lim x→2
(x + 2)(3x -2) (x - 2)(√x + 2 + √3x - 2) lim x→2
-2x + 4 (x - 2)(√x + 2 + √3x - 2) lim x→2
-2 Pada soal No.6 kita gunakan "Metode mengalikan dengan aspek sekawan". Metode ini diterapkan pada limit yang memiliki bentuk akar.
Nah sekarang anda sudah mengenala berbagai sistem dalam menuntaskan soal limit fungsi aljabar. Semoga anda mampu memecahkan soal-soal limit fungsi aljabar lainnya
Sumber https://www.kontensekolah.com/
Nah sekarang anda sudah mengenala berbagai sistem dalam menuntaskan soal limit fungsi aljabar. Semoga anda mampu memecahkan soal-soal limit fungsi aljabar lainnya

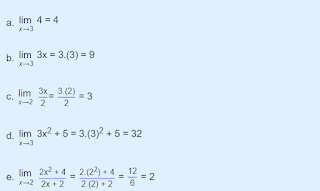




Posting Komentar
Posting Komentar